|
|
|
Michael A. Belessis, Dimitris G. Stamos, Spyros G. Voutsinas
National Technical University of Athens, Fluids Section,
P.O. Box 64070, 15710 Zografou, Athens, Greece
Tel: (+)301-7721096, Fax: (+)301-7721057,
e-mail: aiolos@fluid.mech.ntua.gr
ABSTRACT
The design of a wind turbine rotor is formulated as
a constrainted optimization problem with respect to geometric
as well as operational characteristics. It is required to maximise
the energy production for a given Weibull wind distribution with
constraints on the loads, the tip-speed-ratio and the geometry
of the blade including the airfoil shape. To solve this problem
a method based on a genetic algorithm was developed. Its flexibility
and robustness proved to be significant in giving even higher
performance gains in comparison to classical, calculus-based methods.
Results are presented for three stall regulated machines of different
sizes: 100, 300 and 500kW. Starting from existing wind turbines
as initial solutions, the application of the genetic process gave
a 10% gain in the energy production which is a quite encouraging
result. This is a realisable result since the method selects the
airfoils out of a large data base of realistic airfoils.
Keywords: Optimization | Airfoil Sections | Blades | Cost of Energy
2. FORMULATION OF THE DESIGN PROBLEM FOR NHORIZONTAL AXIS WIND TURBINE ROTORS
3. APPLICATION TO STALL REGULATED ROTORS
The optimal design of wind turbine rotors received lately the attention of researchers and manufacturers in view of promoting wind energy at all levels [1,2]. The problem is a challenging one because the underlying physics is non-linear. In the general case quite different features have to be brought together into a feasible as well as technically and physically acceptable context. So the design problem can become quite complicated.
Due to the complexity of the problem, traditional methods of optimization as the gradient methods, will find difficulties in providing solutions either because the computations involve singularities or because local minima or maxima will trap the computational procedure. In order to overcome the difficulties and still have a flexible and robust design tool, genetic algorithms (GA) were considered [3], [4],[5].
Genetic algorithms were initially introduced by computer scientists as a constructing technique for computer programs and consequently they were used as optimization tools. They are based on the natural selection and the characteristic reproduction mechanisms of living organisms. By definition they try to mimic the natural selection and the reproduction mechanisms of living creatures. The optimizing procedure (Fig.1) has two major parts:
This procedure is continued for several generations, until convergence is reached.
The way that the new generations are created, gives to GA the ability to handle all type of parameters: functions, data bases, logical variables, etc. Also, the evaluation procedure overrides by its self any difficulty due to discontinuities of the cost function or the constraints. This is because unlike calculus based optimization algorithms, GAs do not use gradient type or local searching schemes but scan a whole set of possible solutions.
There are different types of genetic algorithms. They can be classified in two basic categories: those based on binary crossover schemes and those using continuous analogues (Fig. 2). In the first case all characters are recorded to form a binary string. Binary strings are used for each variable separately and then combined to give the total string or chromosome. A 10-bit string is capable of representing 210 different combinations which can be sufficient to represent the variation of a variable. The reproduction procedure is carried out by the mechanisms of crossover and mutation. Take two parents. Cut their chromosome at a crossover point and then crossover the parts to get two children. After crossover mutation will change randomly with a small probability (typically 0.001) the characteristics of the children and thus create the next generation. This procedure although attractive is not suitable for continuous varying characteristics. In this case a different procedure can be followed. Let A1 and A 2 be the rotor diameters of two turbines to be considered as parents. Then the rotor diameter of the children will belong to an interval defined by the two initial values plus a buffer: [A1-a, A2+a]. The specific values can be chosen randomly until the predecided number of children is reached. In the method developed this approach was used.
Genetic algorithms evolve in a monotonic way. In the case of the optimal design of wind turbine rotors, the method produces better and better machines (Fig.3). The rate of convergence is slow. A typical run would require some thousands of direct calculations (Fig. 4). Compared to calculus based methods there is a relation of 1:30 in terms of computational effort. Note that for the same amount of effort, a Simplex method will give a better solution which however is not the best possible.
The rotor design problem is formulated as a constrainted optimization problem as follows:
DEFINITION OF THE COST FUNCTION. The cost function can be a weighted combination of the different characteristics such as the energy production, the mass of the blade, the level of emitted noise, etc. The weights in such an expression indicate the perspective the design should have.
SELECTION OF CONSTRAINTS. Suitable constraints are essential for resulting to acceptable designs. The requirement of a blade to meet strength requirements leads to a constraint expressed for example by limiting the maximum of the flapping moment at root. Another option can be to sustain the survival wind velocity (70m/s for a type I machine). One more constraint often needed concerns the tip-speed-ratio which must be smaller than about 60m/s. Other constraints can be set on the geometry of the blade so as to get meaningful shapes. For example the chord distribution must be a decreasing function of the radius.
SELECTION OF THE DESIGN VARIABLES. In order to complete the formulation the designer must choose the design variables which will be determined by the solution of the optimization problem. As design variables can be used: the chord and twist distribution, the fixed pitch or the pitch variation strategy according to the concept of the machine, the rotational speed, the rotor diameter, the shape of the airfoils, the thickness and composition of the skin of the blade.
All aerodynamic calculations were performed with RAFT (Rotor Analysis Fast Tool), a blade element model [6].
Since the primary target of rotor optimization is high energy efficiency, the choice of the airfoils is essential. In order to parametrise this "difficult" design variable two different alternatives were examined. The first choice was to use analytically parametrised lift and drag curves with free parameters the maximum lift, the maximum lift angle, the minimum drag, etc. Because it is not guaranteed that the target lift and drag can be attained, a second approach was also considered according to which the GA selects airfoils from a data base of real ones. This database was constructed by creating airfoils of minimum drag to lift ratio for a certain lift coefficient using an airfoil shape optimization code [7].
In order to verify the behaviour of the method some preliminary tests were made including the optimization of the same initial rotor for different wind potentials. It was observed that GA results in rotors with P-V curves adapted to the Weibull distributions. This can be noticed by the position of the power peak (Fig 5). Also, it was noticed that the rotor designed for high wind speeds performs well also at sites of low mean speed. This agrees with the conclusions of Selig [5].
Next the method was applied to three stall regulated wind turbines of different sizes: 100kW, 300kW and 500kW. Existing rotors were used for the definition of the initial machines. In order to have comparable results all calculations were performed with the same parameters.
Different design alternatives were considered. A summary of the tests is provided in Table 1. Columns correspond to different choices of design variables. In the lower part of the table the gain of the energy production with respect to the performance of the initial machines is given in per cents. The dash indicates to insignificant gain whereas blank cells correspond to runs that were not performed. The Weibull distribution used corresponds to a mean wind velocity of 7m/s. Columns 1-14 correspond to runs with the maximum power constrainted by the rated power of the initial machine. Column 15 is different. Instead of limiting the maximum power of the rotor, an upper limit for the maximum flapping moment at the root was set. This limit was chosen to be the maximum flapping moment of the initial rotor. When the power is constrainted, optimization has the tendency to:
(a) select airfoils with increased maximum lift coefficient (Fig 7) but this trend is reduced when rotor diameter is set free.
(b) refine the P-V curve significantly when the rotor radius is set free(Fig 6). This also results to thinner blades (Fig 8).
It must also be noticed that the free selection of airfoils lets GA to produce better rotors with P-V curves in their whole range, both before and in the stall region.
From a methodological point of view the experience with genetic algorithms was absolutely convincing. They are flexible, not only because of their ability and easiness of handling difficult problems but also for their better rotors as compared to those obtained by means of conventional optimization methods. In particular genetic algorithms are so to say tailored made for global optimization which should be considered in order to reach the best possible results. The possibilities with such an approach especially when also control characteristics are included will be considered in the future.
From the practical point of view and according to the results obtained so far it can been concluded that an increase of at least 5% to the energy production of current wind turbines is certainly realisable by only modifying the airfoil shapes. There are indications that this increase can reach up to 15% so that a target of 10% can be expected when all parameters are included in the design.
This work was partially financed by the Greek General Secretariat of Research and Technology under the contract EPET-II #573. The authors would like to thank Dr P.Chaviaropoulos (CRES) for the very interesting and valuable discussions.
1. P.L.Fuglsang, H.A.Madsen, RISOE Report I-830(EN)
2. P.Chaviaropoulos, Inverse Problems in Engineering (1996) to appear
3. D. Beasley, D.R.Bull, R.R.Martin, University Computing 15 (1993) 58 (part 1) and 170 (part 2).
4. K. KrishnaKumar, AIAA Paper 93-0315 (1993).
5. M.S.Selig, V.L. Coverstone-Caroll, ASME Journal of Energy Resources Technology 118 (1996) 22
6. K. Katopis, S. Voutsinas, NTUA Report (1996)
7. P. Chaviaropoulos, A. Vossinis, S. Voutsinas, EUWEC'96 (1996)
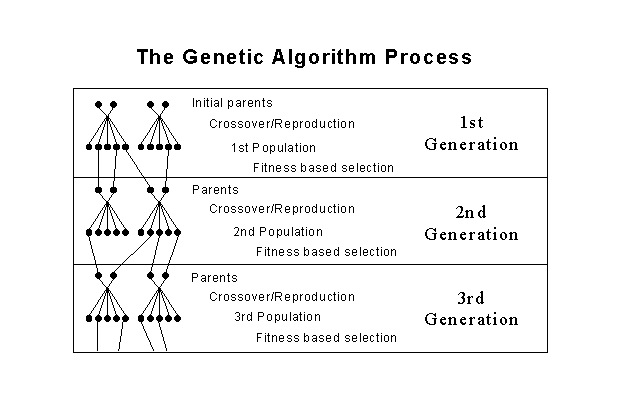
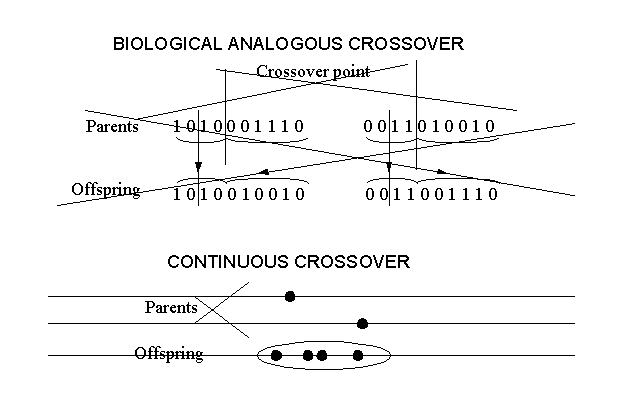
Figure 2: The binary and continuous crossover schemes
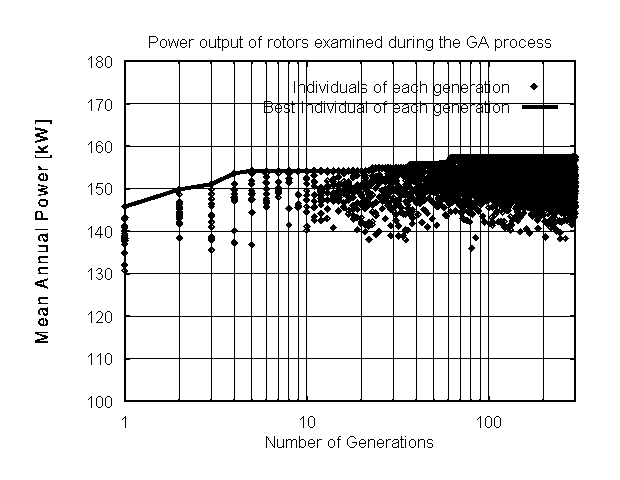 Figure 3:
The evolution of the population during the GA process.
Figure 3:
The evolution of the population during the GA process.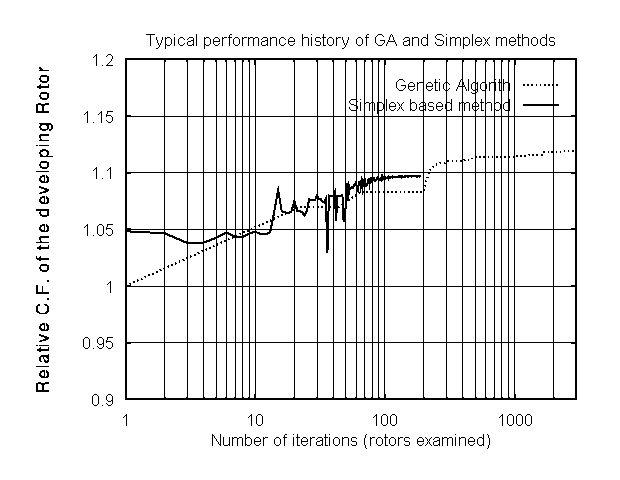
Figure 4: Comparison of a Simplex based and a GA optimization method.
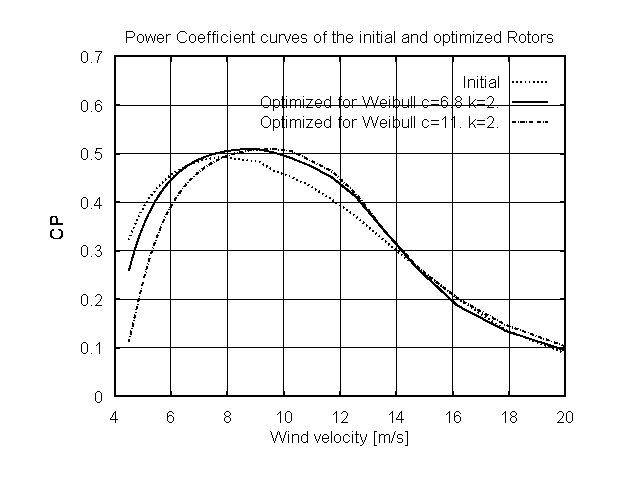
Figure 5:The performance characteristics of an initial and two optimized rotors for different Weibull distributions.
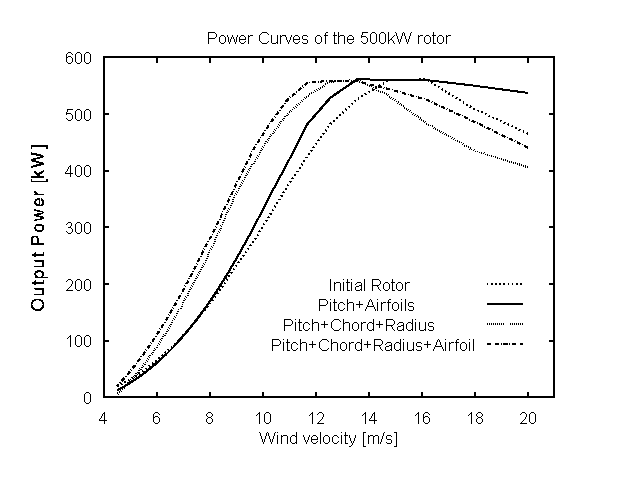
Figure 6:The performance characteristics of optimized rotors optimized to different design alternatives.
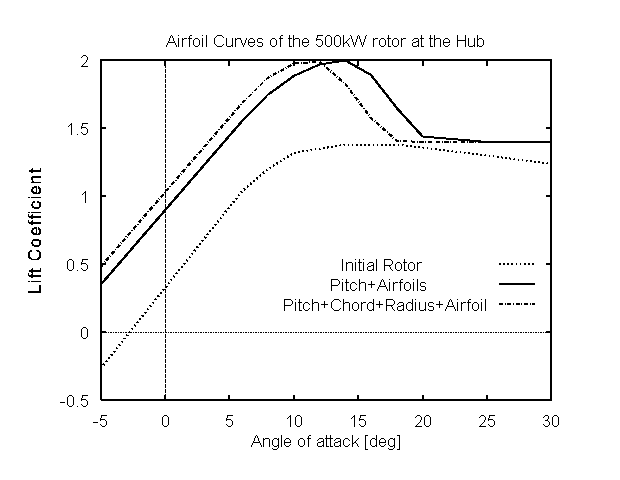 (a)
(a)
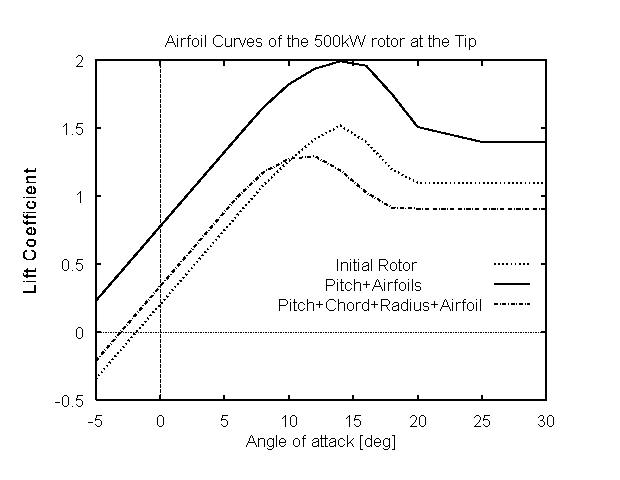 (b)
(b)
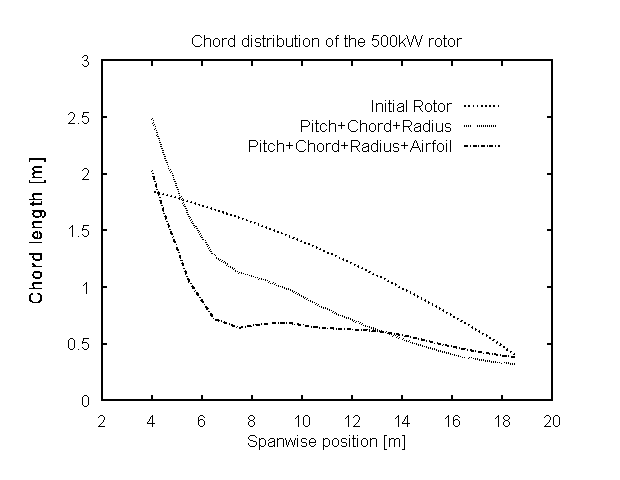
Figure 8: The spanwise cord distribution of the optimized rotors.
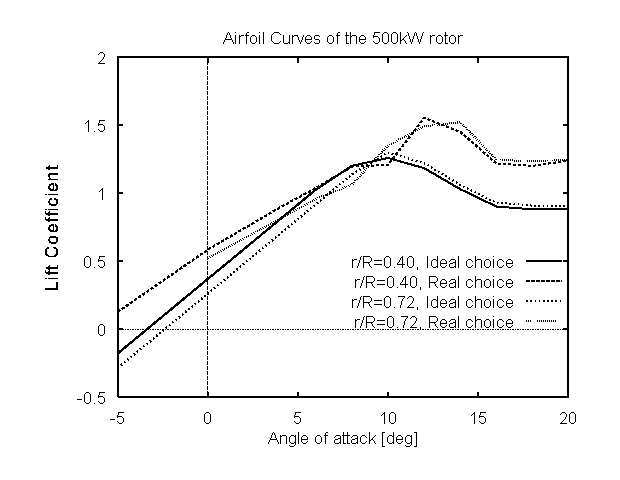 (a)
(a)
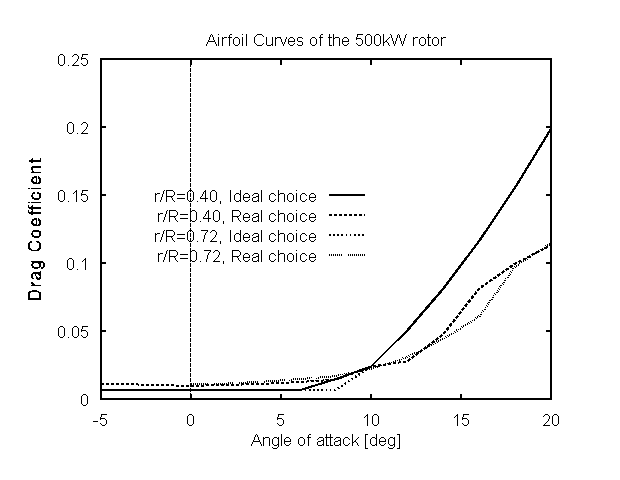 (b)
(b)
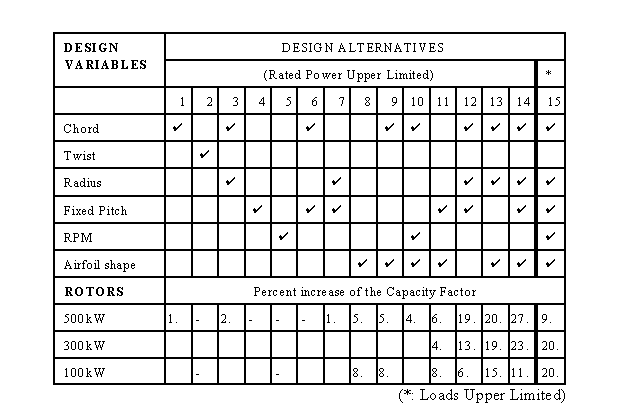 Table 1:The design alternitives investigated.
Table 1:The design alternitives investigated.
|
|
|
|
|
|