|
|
|
P.I. Chassapoyannis(a), T.P. Philippidis(b), S.G. Voutsinas(a)
(a) Department of Mechanical Engineering, Fluids Section
National Technical University of Athens, P.O. Box 64070, 15710 Athens, Hellas
(b) Department of Mechanical Engineering, Section of Applied Mechanics
University of Patras, P.O. Box 1401, 26500 Patras, Hellas
and
Center of Renewable Energy Sources,
19km Marathonos Avenue, 19009 Pikermi, Attiki,
2. DESIGN & EVALUATION OF WT ROTOR BLADES:
3. DEFINITION OF AN ADVANCED AEROELASTIC MODEL
Aeroelastic calculations constitute an indispensable part of the design of a wind turbine. Until recently, only simple models were used in close connection to experience. As a result the design very often turned out to be overdimensioned. In some cases even complete failure of blades has been reported in 1993 and 1994. In view of advancing the design of wind turbines, the development of more elaborate tools was initiated in several European countries. In Hellas this task was undertaken jointly by CRES (Center of Renewable Energy Sources), NTUA (National Technical University of Athens) and UP (University of Patras) within the framework of a wide collaboration in European as well as National research projects. It consists of combining experience and know-how aiming at developing well validated advanced models. In the present paper the results of the definition and evaluation phase of this process are reported.
Survey of the Current State of the Art
Wind turbines operate in a hostile environment where strong flow fluctuations can excite intense vibrations, which in their turn would eventually cause fatigue failure. The study of this problem requires computational tools that model the coupling of aerodynamics, structural dynamics and wind turbulence. Since reliability is always undisputable in engineering, wind turbines are checked thoroughly. A long series of load cases must be simulated according to standards set by international boards [1], [2]. Next the results are synthesized either as extreme or as fatigue loads to be used in combination with specific design criteria which the turbine must satisfy.
Very often simple explicit relations are used [1]. Because the design must be at the safe side, all load calculations are set to their upper limits whereas high safety factors are added to guarantee the operation of the turbine over a long life time. Designs based on such simplified procedures, can become overdimensioned leading to high costs. Optimisation of the design requires more accurate estimations of the loads and therefore more elaborate models have to be used.
Several alternatives exist ranging from simple up to sophisticated engineering tools. Most of them were developed over the last few years at DEWI (Germany), ECN (Netherlands), FFA (Sweden), Garrad & Hassan (United Kingdom) and RISO (Denmark). Their core is a conventional blade element aerodynamic model coupled with a beam structural model. Recent research work on such models concluded that they need upgrade especially in terms of aerodynamics [3]. The latest relevant developments on aerodynamics were included in [4] and [5]. In this activity we contributed with three aerodynamic models of varying complexity. Starting from a very detailed free-wake aerodynamic model that approximates the wake with vortex particles (GENUVP, [6]), we produced a lifting surface model with a semi-prescribed wake (LSURF, [5]). At a second step, aerodynamics were further simplified giving an improved blade element model (RAFT, [7]). The computational requirements of each model are proportional to its complexity: for a 10min time series run the free-wake model needs several days, the prescribed wake model requires one day, whereas the advanced blade element model needs only 10 min.
In Figures 1, 2 the three aforementioned models are compared with full scale measurements and predictions from a conventional blade element model. All results were obtained using a standard beam model to account for the blades flexibility, so any difference is purely aerodynamic. The predictions concern the flapwise and edgewise moments at the blade root of the TJAEREBORG 2MW HAWT (Denmark). Figure 1 presents two cases where the pitch of the blade changes: (a) wind speed: 7.4m/s, pitch step: from 3o to 1o in 2.1sec, (b) wind speed: 12.5m/s, pitch step: from 3.19o to 1.16o in 1.1sec. Figure 2 presents two cases of yawed operation at 8.5m/s wind speed (-3o and 32o respectively).
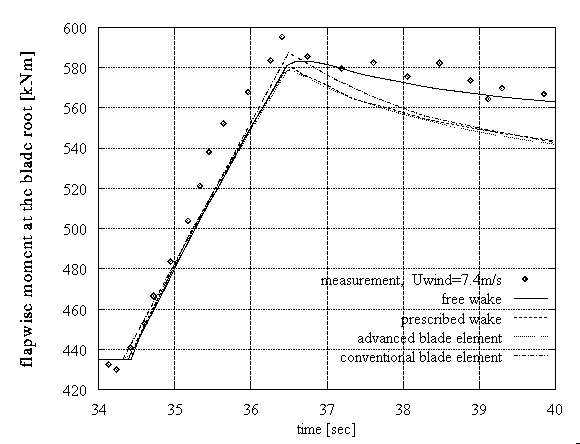
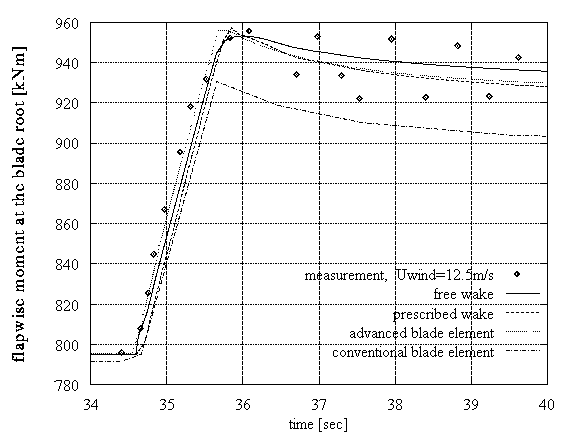
Figure 1: Fast pitch steps: comparison of prediction tools performance
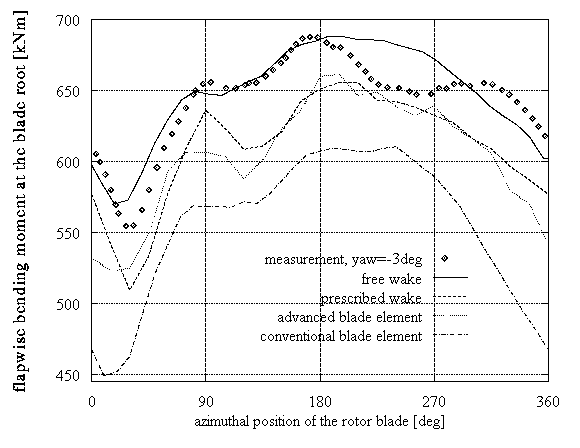
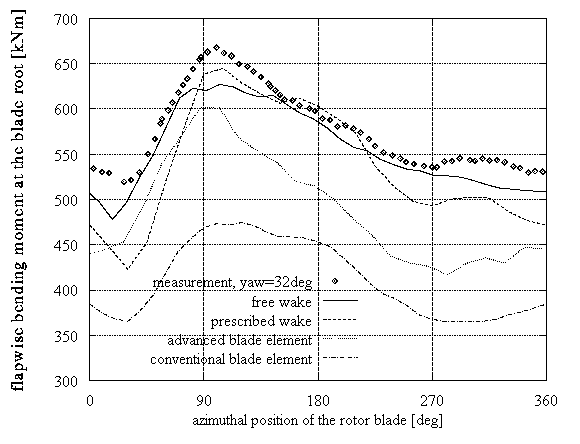
Figure 2: Yawed operation: comparison of prediction tools performance
The accuracy of the models appears proportional to their detail. The best predictions are those from the free-wake model, whereas the less accurate are those from the advanced blade element, which nevertheless behaves better as compared to the conventional blade element model.
Flexibility of the blades can be modelled either by one-dimensional models based on classical beam theory or by thick shell-type models. Because blades are made of composite materials a shell type model is certainly preferable. However, its computational cost makes the use of shell models prohibitive in a design 2rocedure (a 10min time series run would require several days). So, we need to rely on beam models. The lack of a standard method for defining the equivalent beam data for a blade is the main weakness of structural modelling of wind turbines with beam type approximations. In order to override this problem, a homogenisation procedure was applied in combination with a module which projects the three-dimensional thin-wall structure of a blade on its beam equivalent, taking into account the stacking sequence layout of its construction (PROBEAM, [8]).
Aeroelastic simulations are based on coupling the aerodynamics with structural dynamics both kinematically and dynamically. The rates of deformation are communicated to the aerodynamic part as additional excitation term in the kinematic boundary condition. On the other hand aerodynamic loads are communicated to the structural model of the blade (dynamic coupling). These two conditions are satisfied simultaneously in order to have full coupling. Within this context separate tools were synthesized to give an advanced aeroelastic model. An step by step description of such a procedure is as follows:
The simulation methodology described above, was applied to the rotor blade of DEBRA-25 100KW HAWT (Germany) [9], [10]. This blade is made of two parts of the same length, 5.8m, joined together with a flange. The overall blade length is 11.6m and its nominal weight is about 280kg.
First, a static test was simulated. Concentrated loads were applied at the shear center at specific sections (9.0kN, 9.39kN, 4.76kN and 8.28kN at 2.14m, 4.6m, 6.85m and 9.35m respectively from the blade root). The loads had an inclination of -15o with respect to the edgewise direction. For the shell modelling of the blade the commercial software NISA-II of EMRC was used [11]. NISA-II is a thick 3D-component shell element model, that defines 8 nodes per element and 6 degrees of freedom per node. The equivalent beam data "beam_0" given by PROBEAM after homogenisation of the blade structural characteristics, gave the results shown in Figure 3. Even though the flapwise deflection was well predicted, the edgewise stiffness had to be modified. A uniform reduction of 39% was introduced (also the flapwise stiffness was increased by 3%), leading to the "beam_1" model. The comparison of the radial distribution of the flapwise and edgewise deflections between the "beam_1" and "shell" results was quite good (Figure 3).
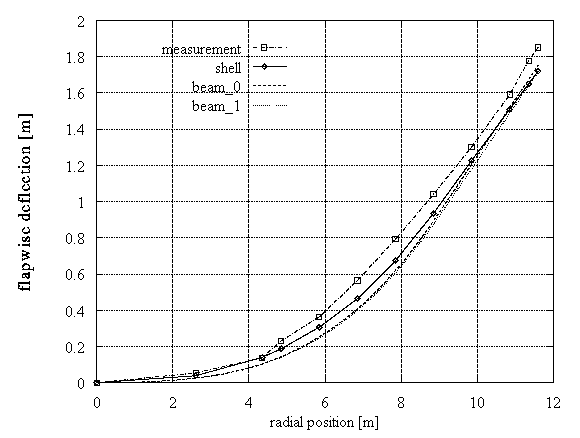
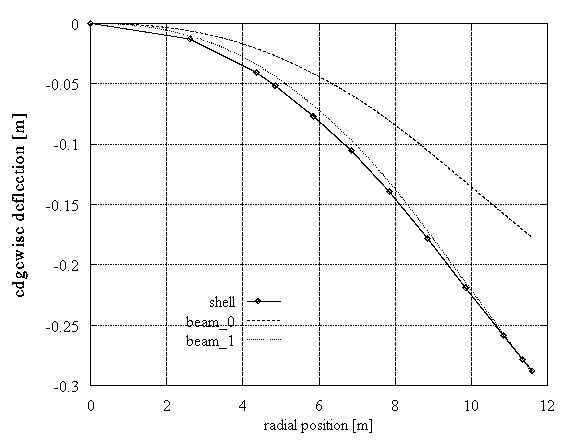
Figure 3: DEBRA rotor blade, static loading
As regards dynamics, in order to reach the eigenfrequencies of the "shell" model a uniform reduction of the mass by 6% was made at the "beam_1" data set (Table 1). Next, two dynamic tests were considered for the "beam_1" model. Again, the loading was consisted of concentrated forces at specific positions. Zero initial conditions were put for the deflection and its spatial and time derivatives. For the time integration of the dynamic equations the Newmark method was used with settings: â=0.3025, ã=0.6, time step=0.025sec.
| eigenfreq.[Hz] | measured | shell | shell | 'beam_1' | 'beam_2' |
| 1st flapwise | 2.19 | 2.326 | 2.226 | 2.323 | 2.322 |
| 1st edgewise | 3.68 | 3.466 | 4.004 | 3.229 | 4.210 |
| 2nd flapwise | 5.87 | 6.005 | 5.865 | 6.132 | 6.115 |
| 2nd edgewise | - | 11.11 | 12.653 | 10.419 | 13.320 |
Table 1: Eigenfrequencies of the DEBRA rotor blade.
In the first test, a concentrated but time varying load was applied at 7.35m for 0.15sec. From 0sec to 0.05sec the loading was linearly increasing from 0kN to 5kN, then up to 0.1sec the force remained constant and then decreased linearly to zero at 0.15sec. The shell and the beam predictions were found to be in good agreement (Figure 4): the two results are close as regards the phase and the amplitudes; both transients have similar damping, which is due to the numerical time integration.
The second test concerned the case of an axial gust. The inflow velocity increased from 8m/s to 12m/s in 1sec. Now, the excitation is of aerodynamic origin. In this simulation, the centrifugal and gravitational effects were not taken into account, in order to simplify the test. The loading is similar to a ramp function. Additionally, in order to perform this test with zero initial conditions, the steady state loads corresponding to 8m/s were subtracted from the dynamic part of the loading. Again the beam and shell predictions match well as regards the flapwise deflection. However, a significant difference in level of about 30% was found for the edgewise deflections (Figure 5).
In order to better understand the "beam_1" results, an additional static test was performed, where for a constant inflow velocity at 12m/s the loads were given again from the aerodynamic model. The two predicted flapwise deflections are in good agreement, whereas a big difference appeared in the edgewise deflections at the tip (Figure 6).
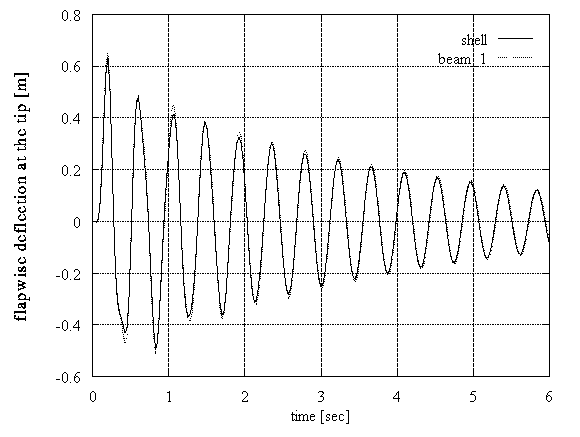
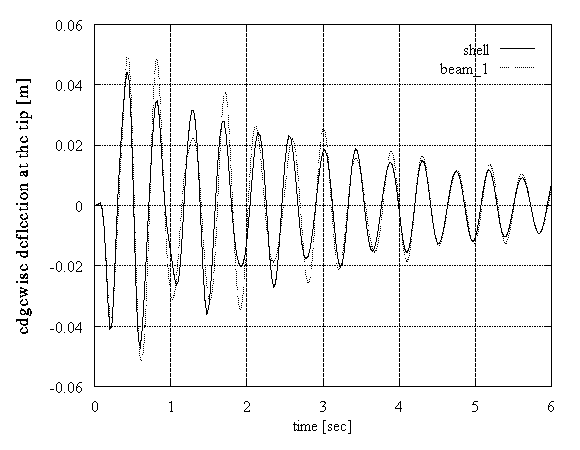
Figure 4: DEBRA rotor blade, dynamic loading
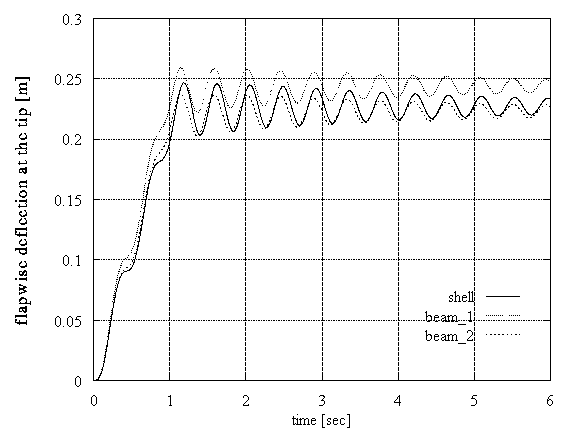
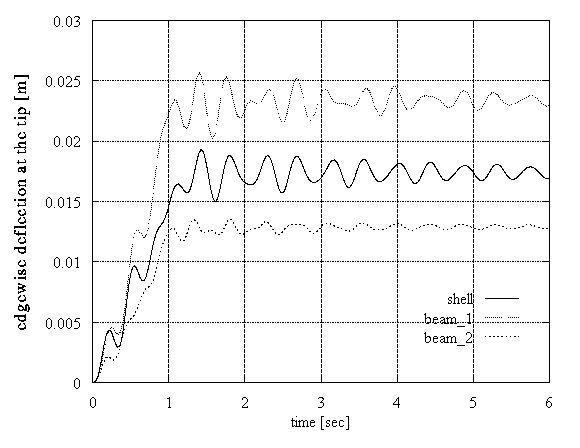
Figure 5: DEBRA rotor blade, dynamic loading
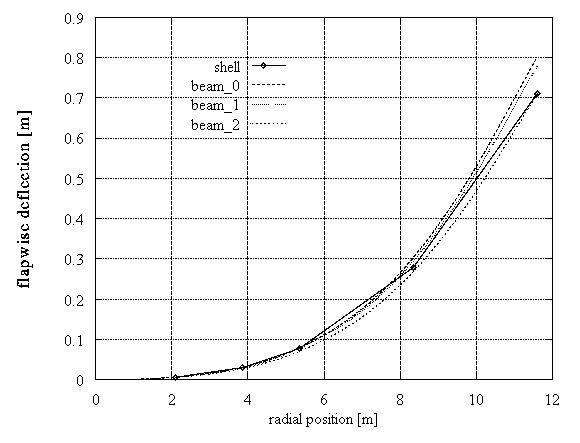
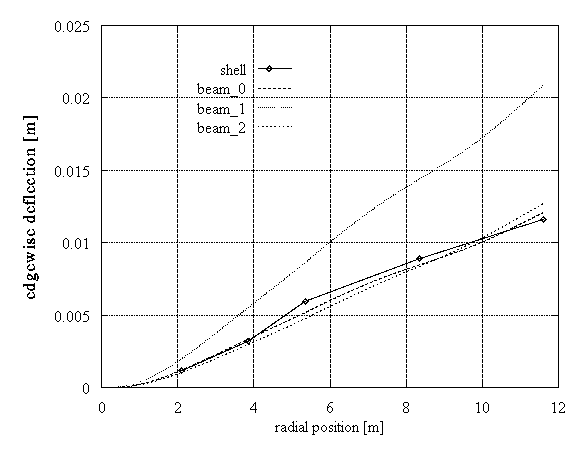
Figure 6: DEBRA blade, static loading
Comparing the results of the produced beam data sets we notice that the flapwise deflection and eigenfrequencies are always well approximated. This was not the case for the edgewise deflection. In the first static test the difference between "beam_0" and "shell" results was significant, so the data had to be corrected. In the second static test the difference between the "beam_1"; and the other models is small in absolute terms, although important as relative error. Similar notes can be done also for the dynamic cases. The "beam_1" eigenfrequencies are closer to the "shell" results, than those from the other beam models. It is important to tune the beam model so as to approximate well the eigenfrequencies of the blade, otherwise it is not possible to predict its dynamic response. As a general conclusion we can say that a fine tuning of the structural characteristics of the blade can be achieved with the "beam_1" data set.
Completing the study for the DEBRA blade we present coupled aeroelastic results from the simulation of a realistic test case with turbulent inflow. A wind simulator based on Veers' model [12] generated the time series of the wind velocity over the rotor disk. A typical case of the wind turbine operation was simulated (wind speed at the hub height: 9m/s, yaw misalignment: -10o, wind shear corresponding to ground roughness: 0.01m). The results for this case are shown in Figure 7, where the spectra of the flapwise and edgewise bending moments are presented. The tower was not included in the structural part, neither the drive train was modelled, due to lack of sufficient data. This explains the difference between the predictions and the measurements in the edgewise bending moment at 4f oHz (fo is the rotational frequency). In general the predictions and measurements are in a good agreement.
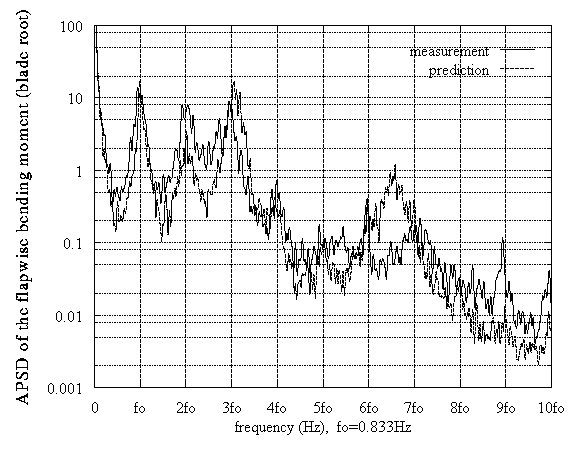
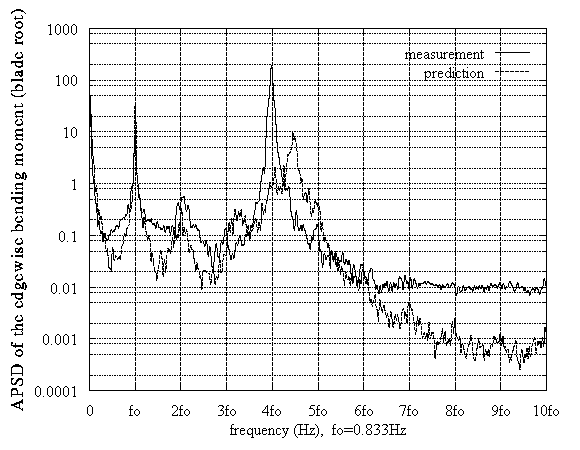
Figure 7: DEBRA HAWT, stochastic case, Uwind=9m/s, yaw=-10o
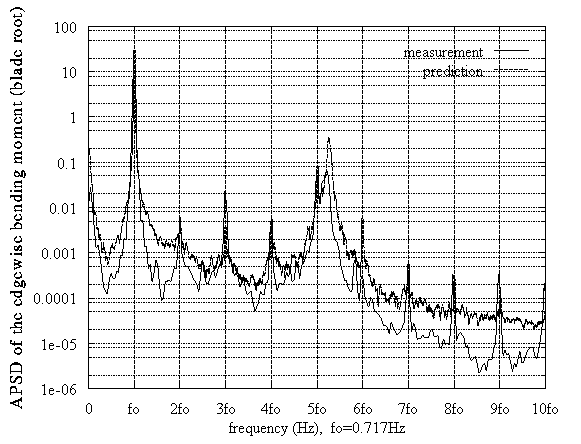
Figure 8: VESTAS HAWT, stochastic case, Uwind=10m/s

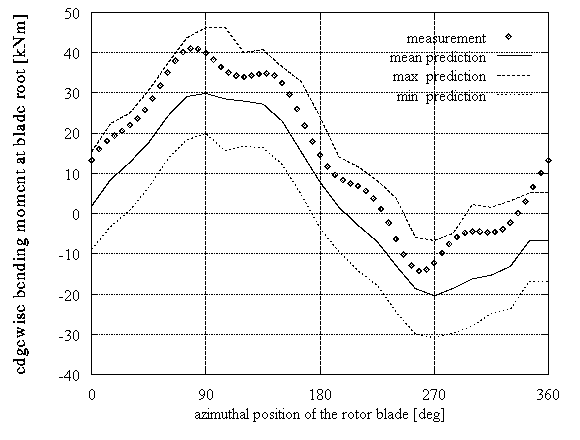
Figure 9: VESTAS HAWT, stochastic case, Uwind=14m/s
The NISA-II package was used as a design tool in order to reproduce the DEBRA rotor blade structure based on detailled structural description of the blade in combination with measured eigenfrequencies and deflections. This is an identification procedure which could be useful in different applications.
The beam approximation was evaluated and found adequate provided that the details of the 3D structure are taken into account. The simulation of a composite blade is possible using a procedure based on the homogenisation of its elastic characteristics. Its fine tuning must be done through a series of simple static and dynamic loading cases.
Three aeroelastic models were used giving satisfactory results especially as regards the ranges of load variations. Differences appear as regards the mean values which are attributed to the incapability of the simpler models to include non-linear effects. RAFT is capable on providing consistent load predictions at very low computational cost. LSURF is a reliable model not depending on empirical data which will work effectively as an engineering tool on modern workstations. Finally, GENUVP proved to be a valuable tool for reference calculations.
Having tested the model on various wind turbines, we feel confident with the predictions. Further tests must be done in order to better understand the behaviour of a wind turbine, to attempt integrated design and finally proceed to fatigue testings which seem to be extremely important for wind turbines operating in complex terrain as is the case of most windy site in our country.
This work was partially financed by the CEU under the JOUR-0083, JOU2-CT92-0113 contracts and General Secretariat for Research and Technology under the EPET-II#573 contract. Also, we would like to thank DLR and DEWI for kindly providing all the detailed data for the DEBRA blade.
[1] Germanischer Lloyd, Rules and regulations, VI - Non-marine Technology, Part 1 - Wind Energy (Hamburg, 1993).
[2] IEC International Standard, Wind Turbine Generator Systems, Part 1: Safety Requirements (CEI/IEC 1400-1, Geneva, Switzerland, 1994).
[3] Grol van, H.J., Snel, H., Schepers, J.G., Wind Turbine Benchmark Exercise on Mechanical Loads, A State of the Art Report (ECNC91030/31, 1991).
[4] Snel H., Schepers J.G., Joint Investigation of Dynamic Inflow Effects and Implementation of an Engineering Method for Response Calculations (ECN, Final Report JOUR-0083, ECN-C-94-107, 1995).
[5] Voutsinas S.G., Development of a New Generation of Design Tools for Horizontal Axis Wind Turbines (NTUA, Final Report JOU2-CT92-0113, Athens, 1995).
[6] Voutsinas S.G., Belessis M.A., Rados K.G., Investigation of the Yawed Operation of Wind Turbines by Means of a Vortex Particle Method (75th AGARD Fluid Dynamics Panel Symposium on: Aerodynamics and Aeracoustics of Rotorcraft, Berlin 1994).
[7] Fragoulis A. (Ed), Development of Hellenique Technology for Wind Turbines of 400-500kW and simultaneous development of Technology for the Construction of Wind Turbine Blades (1st & 2nd six-month progress report, EPET-II#573, Hellas, 1996).
[8] Philippidis T.P., Vassilopoulos A., Katopis K.G., Voutsinas S.G. PROBEAM: a software for fatigue design and analysis of composite rotor blades (2nd National Congress on Computational Mechanics, Conference Proc., Chania, Hellas, 1996).
[9] Bohnisch H., Hald H., Kensche C., Kussmannn A., Molly J.P.
and Seifert H. Entwicklung, Bau und Betrieb Einer 30/100KW Windkraftanlage
(DFVLR-Mitt. 88-06 Stuttgard, Germany, 1988).
[10]
[11]
[12]
[13] Mouzakis F., Morfiadakis E., Fragoulis A., V27 WT Characterization on Andros Site (CRES, Draft Report, 1996).
|
|
|
|
|
|